See the video of the weinar here
The knowledge space approach has become popular because of its clarity, empirical ease of usage, and its usefulness. However, the present paper points out that working with these “knowledge spaces” is much less straightforward and invites scholars to base their work on a number of critical assumptions. In many applications the basis of the knowledge space, a symmetric matrix, is transformed into a network in which nodes represent the activities and related activities are linked with each other. Besides the beauty of their visualisation, network representation of the knowledge space have further been used identify and quantify their structural characteristics by employing measures of social network analyses. This webinar discusses such data manipulations frequently done in the empirical works using the knowledge space. In particular, we point out that some data manipulations have strong implications for the interpretation and scientific use of the knowledge space. More precisely, we seek to highlight three major issues:
- The knowledge space as a network of flows (Flow perspective): Almost by nature, a network induces a conceptualization of flows, i.e., something diffuses through the network along its links. However, the original knowledge space matrix exclusively contains dyadic relational information obtained from the real-world data. We discuss in Section 2 that this flow perspective, for example, inducted by network visualizations, is purely interpretive, since the existence of an actual diffusion process is often not observed.
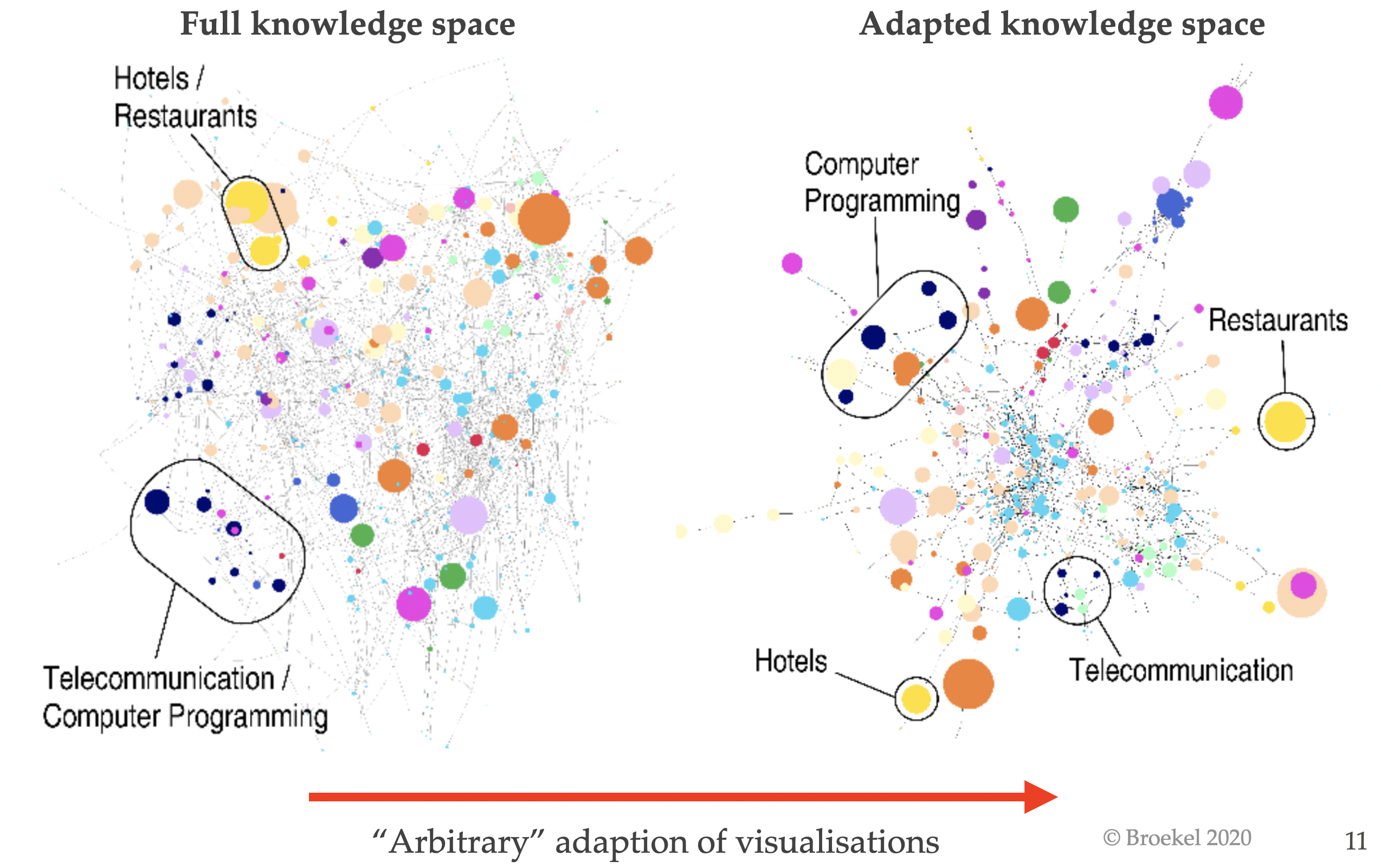
- Thresholds, visualization and shortest paths: To make the network visually more appealing, or to cut ‘insignificant’ connections, often a substantial number of (weaker) relations is removed. Thereby, shortest paths between activities in the network change. The indirect path between two activities (via one or more others) can be longer than the deleted direct path, which was observed in the original data. The visual impression of distance in such a condensed network can lead to utterly false interpretations, which we discuss in Section 3.
- Applying distance-based network measures: Network centrality measures (degree, eigenvector, betweenness, closeness) are increasingly used to describe and analyse knowledge spaces. We argue in Section 4 that in particular metrics utilising network distances are impacted by the translation of the knowledge space to the reduced knowledge network representation.
